Cambiamenti climatici, matematica e pensiero comune

Nel suo trattato “Il Saggiatore” Galileo Galilei scriveva che l’universo è un libro che non può essere compreso se prima non s’impara la lingua con cui è scritto: la matematica. A distanza di quattrocento anni, la matematica è tutt’ora considerata il linguaggio della natura e può dunque venirci in aiuto per comprendere i rapidi cambiamenti negli equilibri del nostro pianeta che si registrano dalla rivoluzione industriale in poi. 

Lo strano fenomeno dei chicchi di grandine oversize

Nella stagione dei monsoni nelle regioni tropicali non è raro che si verifichino violente grandinate, con chicchi che superano facilmente il mezzo chilo. Negli ultimi due anni, però, questo fenomeno è stato osservato anche in Italia. Ma com’è possibile? 

I meteorologi ci dicono che le particelle di ghiaccio presenti in atmosfera in particolari condizioni sono spinte da correnti di aria calda ascendente all’interno di particolari nubi dette cumulonembi, che raggiungono la quota di circa 10 km. Qui, risiedono per un certo periodo e nel frattempo si accrescono di dimensione, proporzionalmente al tempo di residenza a quella quota. 

Siccome l'accrescimento non è impedito in nessuna direzione, la forma del chicco di grandine è completamente simmetrica, che nello spazio equivale a dire che diventa una sfera. Le correnti ascensionali permettono al chicco di grandine di accrescersi a queste alte quote fino a quando la forza di gravità, direttamente proporzionale alla massa dell’oggetto, non supera la spinta verso l’alto. A quel punto, il chicco di grandine cade a terra.

I chicchi che sono caduti recentemente in Italia hanno un diametro di 10 cm ed é stato riportato che il loro peso é di circa mezzo chilo. Vediamo perché.

Il peso del chicco è determinato dal suo volume. Per una sfera (qui occorrono reminiscenze della scuola inferiore e superiore) questo è dato da V = 4/3 per pigreco per il raggio al cubo. Siccome pigreco=3.14 in prima approssimazione semplifica il denominatore della frazione, per cui V= 4 per 5 cm al cubo = 4 per 125 = 500 cm cubici. 

Ora, l'acqua ha densità 1 grammo/(cm cubo), mentre il ghiaccio poco meno (per questo gli iceberg galleggiano in parte negli oceani!). Possiamo dunque dire che il peso del nostro chicco di grandine di diametro 10 cm è di circa 500 grammi.

Fitoplancton, temperatura e possibile estinzione della vita sulla terraferma

Passiamo ora a situazioni più complesse. È facile pensare alle foreste terrestri come ai "polmoni verdi" del pianeta. Gli alberi producono ossigeno, il gas che tutti noi respiriamo, ma non sono gli unici organismi a fare la fotosintesi clorofilliana diurna (mentre di notte emettono anidride carbonica, come noi). Ben oltre la metà dell'ossigeno sul nostro pianeta non proviene infatti dalla terra ferma, ma dagli oceani. Questo è possibile grazie alla presenza di microalghe, diatomee, cianobatteri e altre minuscole forme di vita acquatiche che costituiscono ciò che chiamiamo fitoplancton.

Anche se le loro dimensioni (quasi) non permettono di vederli ad occhio nudo, questi organismi sono ampiamente diffusi negli oceani, che rappresentano il 70% della superficie terrestre. D’altra parte, non tutta la superficie delle terre emerse è occupata da foreste. Ci sono i deserti, le montagne e gli insediamenti antropici che riducono ulteriormente le aree verdi produttrici di ossigeno sulla terra ferma.

Studiare come la velocità di riproduzione del fitoplancton (R) e la sua velocità di produzione di ossigeno (O) variano con i cambiamenti di temperatura diventa fondamentale per cercare di prevedere come cambieranno le condizioni sul nostro pianeta e se ci permetteranno di sopravvivere. Un modello per questa situazione è stato formulato e studiato in diverse pubblicazioni. La figura ne riassume qualitativamente i risultati.

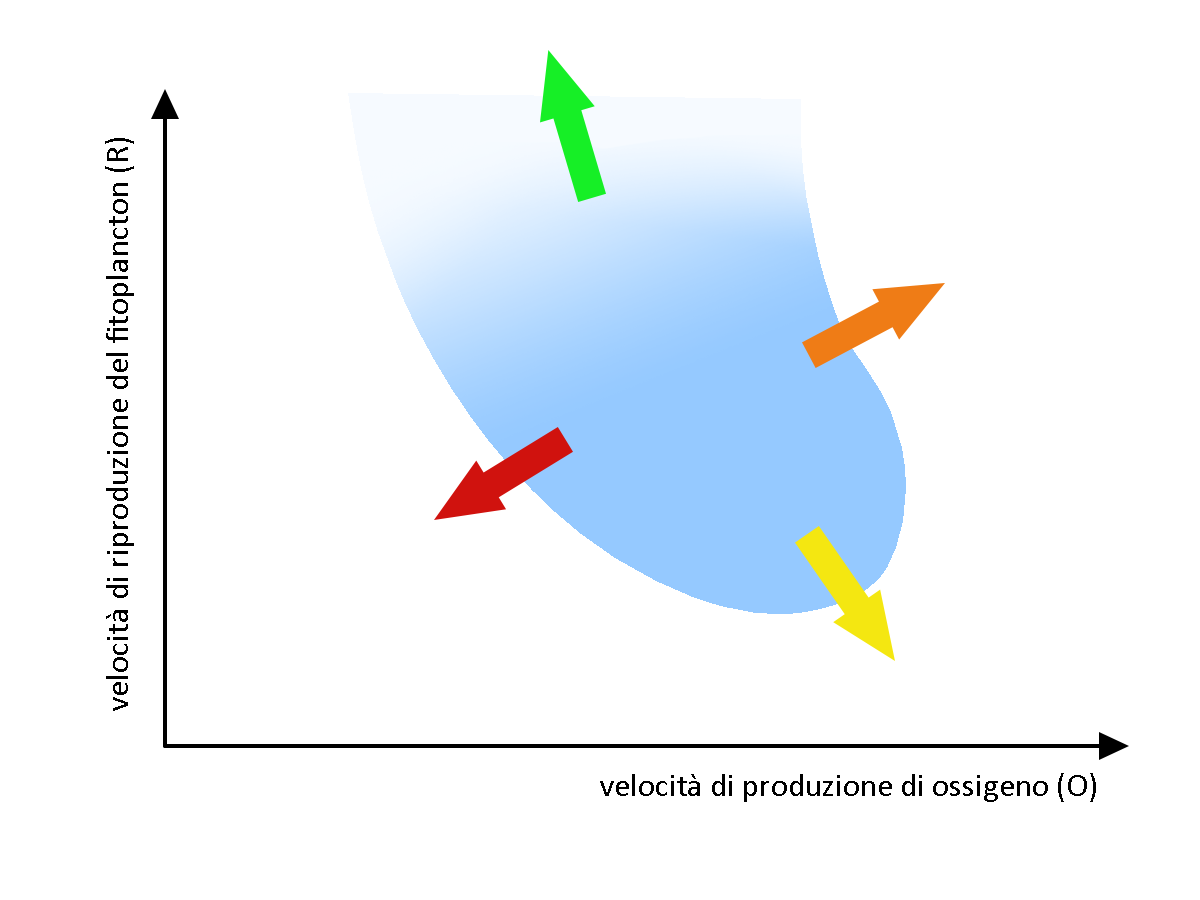
Secondo il modello, nella "penisola" azzurra si hanno le condizioni attuali, favorevoli alla vita sulla terra. In corrispondenza di un aumento di R e diminuzione di O (freccia verde in alto a sinistra), in un intervallo ragionevole, si rimane all'interno della "penisola" e la vita sulla terra non é in pericolo. Se viceversa aumenta O e diminuisce R, si rimane nella zona sicura solo per piccoli cambiamenti, dopodiché uscendo dalla zona sicura si avrà estinzione della vita (freccia gialla in basso a destra).

Nel caso indicato dalla freccia arancione (tanto O e tanto R) si verificheranno (o forse già si verificano?) delle avvisaglie indicanti un'instabilità del sistema, che vira poi verso le condizioni che non permettono la vita. In questo caso, infatti, il raggiungimento del nuovo punto di equilibrio avviene attraverso delle oscillazioni di crescente ampiezza, finché non collassano poi sulla condizione di estinzione delle popolazioni. Questo potrebbe essere un bene, perché forse ci darebbe il tempo di contrastare il fenomeno. Nel caso indicato dalla freccia rossa invece, questi segnali di avvertimento precoce non si verificano e la transizione verso l’estinzione risulta diretta e improvvisa.

I fenomeni oscillanti sono ampiamente diffusi in ambito ecologico, si tratta di situazioni in cui il numero di individui di una determinata popolazione passa ciclicamente tra valori molto alti e molto piccoli. Questo però è pericoloso, perché in natura ci sono perturbazioni stocastiche che possono portare all’estinzione di popolazioni con un numero molto ridotto di individui.

• Mathematical Modelling of Plankton-Oxygen Dynamics Under the Climate Change, Yadigar Sekerci and Sergei Petrovskii, Bulletin of Mathematical Biology, 77(12) :2325--2353, 2015 10.1007/s11538-015-0126-0
• S. A. Vakulenko, I. Sudakov, S. V. Petrovskii, and D. Lukichev (2021) Stability of a planetary climate system with the biosphere species competing for resources. Phys. Rev. E, 103, p. 022.
• I. Sudakow, S. A. Vakulenko, M. Pound, and D. Kirievskaya (2023) Biome stability and fragmentation under critical environmental temperature change. Appl. Math. Model, 114, 189--204.

Fenomeni (quasi) irreversibili in natura

In natura non è raro osservare fenomeni ciclici. Uno degli esempi più noti è forse il caso delle processionarie, che porta ciclicamente serissimi danni alle foreste di conifere americane. Negli ultimi due secoli in Nord-est dell’America si sono infatti osservate esplosioni periodiche della popolazione della processionaria, che si ripetono con una periodicità di alcuni decenni.

Le larve di processionaria sono molto voraci fin dalla nascita e si nutrono delle foglie della pianta su cui sono nate. Il grande numero di individui di questa specie porta dunque a danni serissimi alle foreste di conifere. Una volta defoliate le piante, la popolazione non ha più cibo e si riduce fino quasi a scomparire. Di conseguenza, le piante iniziano a riprendersi. Il tempo in cui gli alberi ricrescono dopo essere stati defoliati dall’insetto é di vari decenni. Quando hanno di nuovo raggiunto una situazione di salute, i pochi insetti sopravvissuti trovano abbondante cibo e la loro popolazione esplode nuovamente, e il ciclo ricomincia. Questo fenomeno è descritto da vari modelli matematici, sviluppati per spiegare la ciclicità di queste ondate di processionaria.

Possiamo però descrivere con modelli matematici analoghi anche altri fenomeni ciclici, come il variare dello spessore dei ghiacci terrestri nel contesto dei cambiamento climatici. In figura troviamo il grafico ottenuto grazie a questo modello. L'asse orizzontale indica la temperatura e l'asse verticale l'altezza dei ghiacci sulla terraferma. In particolare focalizziamo l’attenzione sulla in Groenlandia, dove lo spessore della calotta è di circa 3 Km. Il tempo in questo grafico non compare esplicitamente, ma solo implicitamente, come ora spieghiamo.

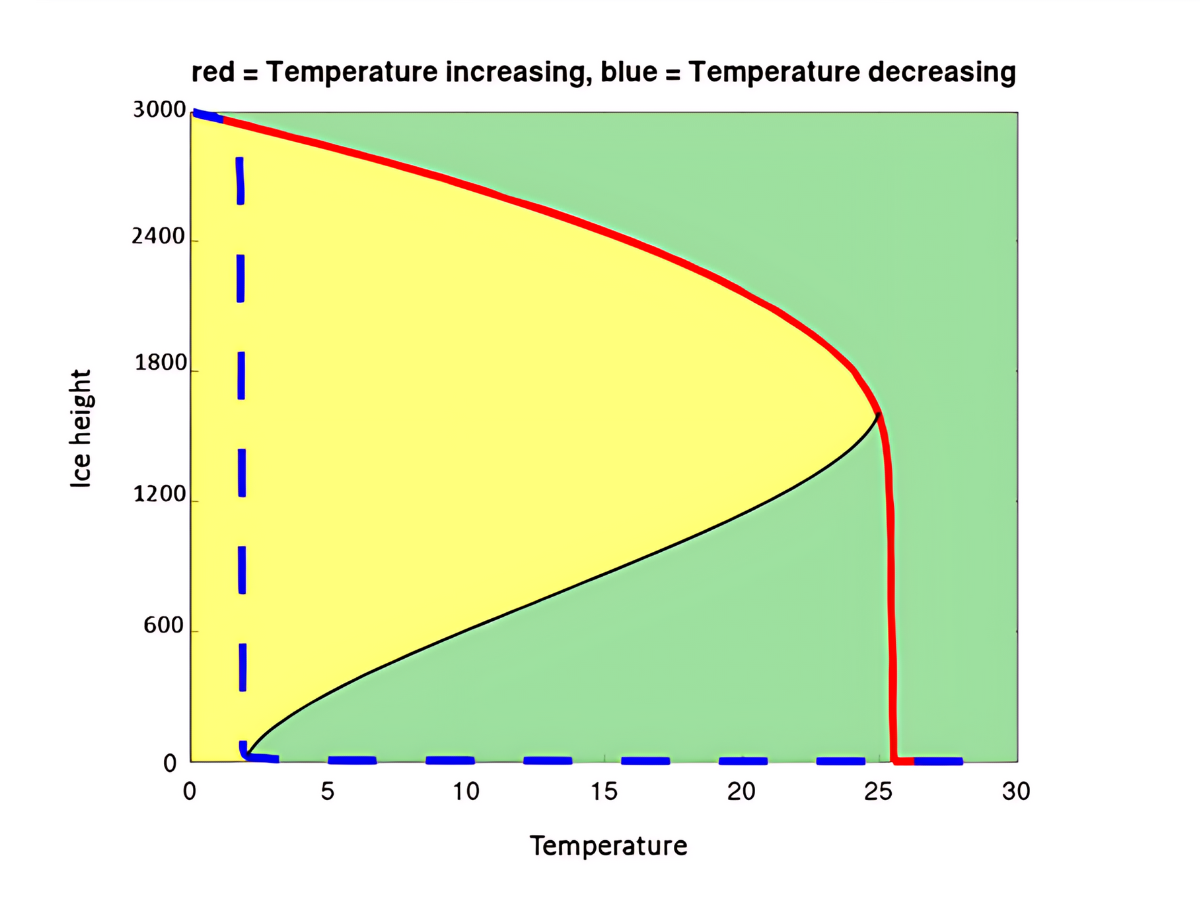
Un punto qualunque nel grafico (non necessariamente sovrapposto alle curve che vi compaiono) rappresenta una situazione con una data temperatura e un possibile livello dei ghiacciai. Il modello che descrive questa situazione mostra però che una situazione che non si trovi lungo le curve non è sostenibile nel tempo. Molto molto rapidamente, data una certa temperatura, il livello dei ghiacciai in figura si sposta verticalmente verso una delle due curve, rossa continua o blu tratteggiata. 

La direzione del movimento è decisa dalla posizione del punto: se è all’interno dell’area gialla si muove verso l'alto. Se il punto si trova all’interno dell’area verde, invece, si muove verso il basso. Pertanto, il sistema sarà, salvo brevissimi intervalli, su una delle curve, rossa o blu, che indicano il livello dei ghiacciai a una data temperatura.

Al momento attuale siamo sulla curva rossa, in un punto diciamo in alto, forse non troppo distante dall'asse verticale. I cambiamenti climatici comportano un innalzamento della temperatura atmosferica. Come conseguenza, le precipitazioni a 3 Km di altezza che in condizioni normali si trasformano in neve e poi ghiaccio, diventano invece pioggia, che scioglie i ghiacci superficiali. Il punto sulla curva rossa allora si sposta più in basso a destra, perché diminuisce l'altezza del ghiaccio e aumenta la temperatura. Questo comportamento continua con l'innalzarsi della temperatura, avvicinandosi al punto critico dove la curva rossa diventa verticale. Qui, un minimo ulteriore aumento della temperatura causa un improvviso collasso del sistema, con lo scioglimento improvviso di tutta la calotta restante. Una grande quantità di acqua dolce si riverserebbe improvvisamente nell’oceano, causando un’ondata con possibili conseguenze catastrofiche almeno per le regioni limitrofe. Ma ci sono altre considerazioni.

Innanzitutto, gli organismi marini non avrebbero probabilmente tempo di adattarsi a un così rapido cambiamento di salinità dell’acqua e ciò porterebbe molte specie all’estinzione. Nell'Atlantico poi c'è una corrente marina, detta AMOC (Atlantic Meridional Overturning Circulation), che risale dai Caraibi lungo la costa dell'America del Nord fino alla Groenlandia e poi si inabissa e ritorna indietro sullo stesso percorso a grandi profondità. Lo scioglimento dei ghiacciai altererebbe la densità dell’acqua dell’Atlantico e potrebbe portare a un cambiamento di rotta o un rallentamento di questa corrente. Ciò potrebbe provocare un raffreddamento degli ambienti costieri, trasformando il clima da temperato al clima che si trova in regioni dove queste correnti oceaniche mitiganti sono assenti.

A parte la discussione degli effetti nefasti di questa situazione, qui voglio considerare invece un punto fondamentale, che nel pensiero comune è trascurato o non è affatto conosciuto. Si pensa infatti che se raggiungessimo una temperatura tale da provocare lo scioglimento improvviso e massivo dei ghiacci superficiali, basterebbe diminuire un pochino la temperatura per tornare alla situazione precedente. Purtroppo, come si spiegato dal grafico in figura 2, questo non è vero. 

Una volta superato il punto critico sulla linea rossa e raggiunta la parte in basso a destra del grafico, anche provando a diminuire la temperatura ci si trova sotto la curva nera, per cui ogni punto qui sotto si assesta verticalmente verso la curva blu. Pertanto, lo spessore del ghiaccio non aumenta. Continuando a diminuire la temperatura, si continuerà a rimanere lungo la curva blu, finché non si raggiungerà l'altro punto critico, dove la stessa ha un'impennata verso l'alto. A questo punto le condizioni attuali saranno ripristinate repentinamente. Ma tutto questo processo avrà bisogno di un tempo molto lungo per realizzarsi, almeno decenni, se non addirittura secoli.

Il sistema climatico è un sistema complesso e, contrariamente a quanto si pensa, se non riusciremo a limitare l’aumento di temperatura al di sotto del punto critico, tornare indietro sarà molto difficile. Con questo esempio, perciò, ho cercato di dimostrare che i modelli matematici permettono di interpretare fenomeni anche controintuitivi e contrastare luoghi comuni che portano a considerazioni assolutamente false. 

• Peter D. Ditlevsen, Susanne Ditlevsen, Warning of a forthcoming collapse of the Atlantic meridional overturning circulation, Nature Communications 14(1) DOI:10.1038/s41467-023-39810-w
• Ohenhen, L.O., Shirzaei, M., Ojha, C. et al. Disappearing cities on US coasts. Nature 627, 108 -115 (2024). https://doi.org/10.1038/s41586-024-07038-3
• Miles, B.W.J., Bingham, R.G. Progressive unanchoring of Antarctic ice shelves since 1973. Nature 626, 785 - 791 (2024). https://doi.org/10.1038/s41586-024-07049-0
• Greene, C.A., Gardner, A.S., Wood, M. et al. Ubiquitous acceleration in Greenland Ice Sheet calving from 1985 to 2022. Nature 625, 523 - 528 (2024). https://doi.org/10.1038/s41586-023-06863-2